加工機で平歯車を作ろうと思い、まずはデータの作成です。φ2mmのエンドミルで加工できる最少のサイズを”モジュール2.0”と見込んで検討しました。最終的な板厚はMAX5mmで、うまくいけば2.5Dのカッターが使えます。
歯数40と歯数12の組み合わせで、歯数12は市販品になるかもしれないので、標準的なインボリュート歯車を適用したいです。
FreeCADの「インボリュート歯車作成ツール」を使ってみるが・・直線のようだ
たまに使うFreeCADに、インボリュート歯車作成機能がありました。早速作画してdxf出力し、図脳rapidにインポートしてみました。
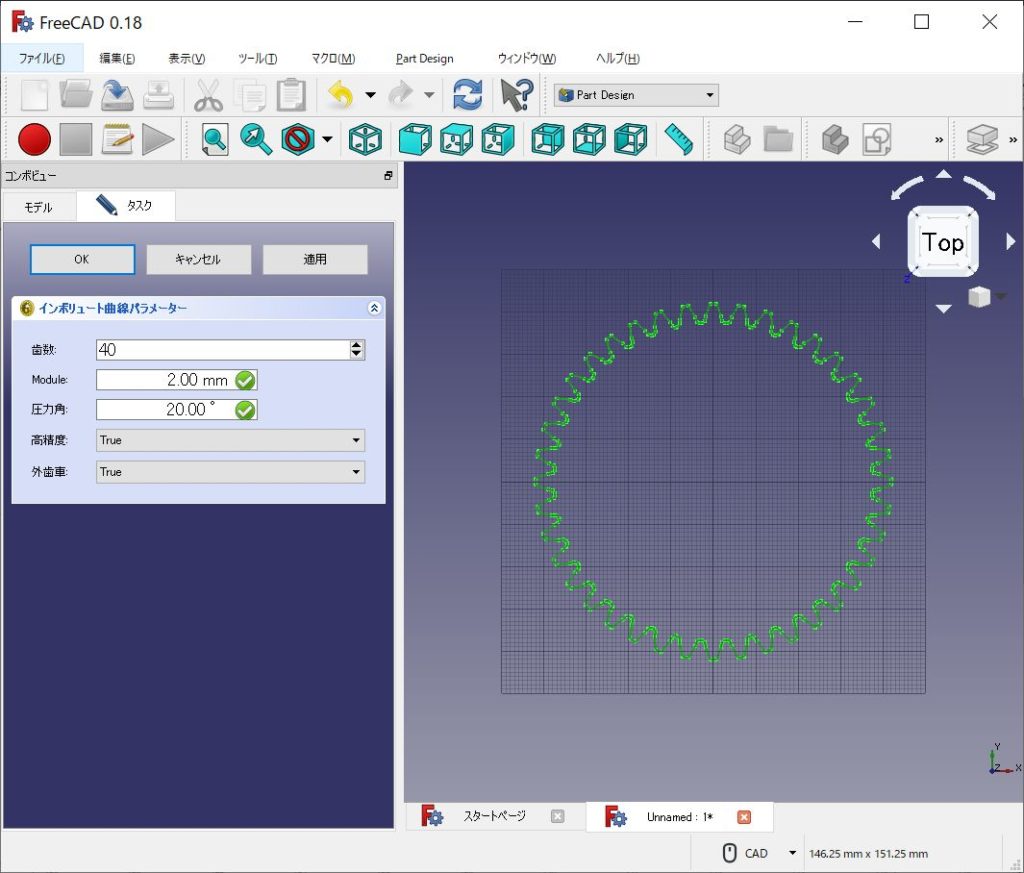
細かく見ると、インボリュートではなく、直線で構成されていました。回転伝導は可能でしょうが、インボリュート歯車との組み合わせはちょっと難がありそうです。※のちにDXF設定で高精細化できることが判明平歯車を作る その3参照。
pythonでインボリュート座標をCSV出力してみる
インボリュート曲線の式は比較的簡単なので、pythonで確認しました。
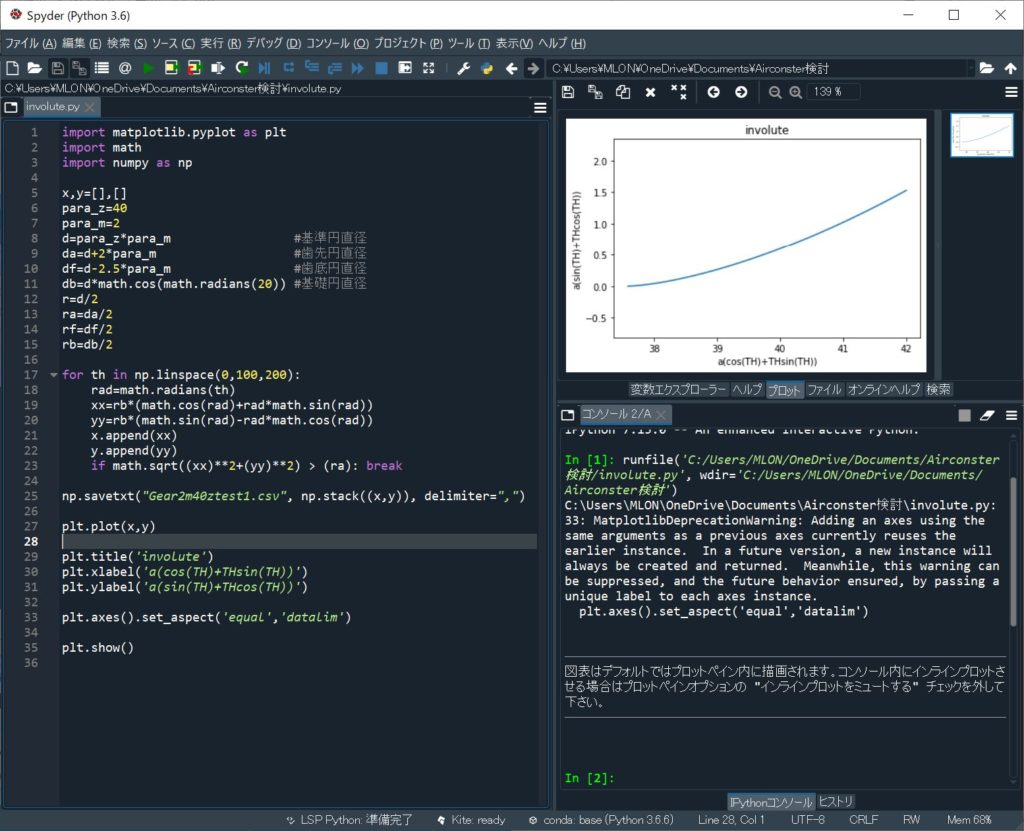
下はモジュール2.0、歯数40、圧力角20°、転移なしの歯車です。パラメータを変更するときは「para_m」「para_z」がそれぞれモジュール/歯数です。
import matplotlib.pyplot as plt
import math
import numpy as np
x,y=[],[]
para_z=40
para_m=2
d=para_z*para_m #基準円直径
da=d+2*para_m #歯先円直径
df=d-2.5*para_m #歯底円直径
db=d*math.cos(math.radians(20)) #基礎円直径
r=d/2
ra=da/2
rf=df/2
rb=db/2
for th in np.linspace(0,100,200):
rad=math.radians(th)
xx=rb*(math.cos(rad)+rad*math.sin(rad))
yy=rb*(math.sin(rad)-rad*math.cos(rad))
x.append(xx)
y.append(yy)
if math.sqrt((xx)**2+(yy)**2) > (ra): break #歯先円超えたらbreak
np.savetxt("Gear2m40ztest1.csv", np.stack((x,y)), delimiter=",") #CSV出力
plt.plot(x,y)
plt.title('involute')
plt.xlabel('a(cos(TH)+THsin(TH))')
plt.ylabel('a(sin(TH)+THcos(TH))')
plt.axes().set_aspect('equal','datalim')
plt.show()
ムムッ、spyderを4.1.3に更新したらなんか使い勝手が違うぞ、プロットがタブになってる~、と思いながらCSV出力をとりあえず作ってみた。基礎円から始まり、歯先円を超えてストップする曲線の座標を計算します。x、y座標をカンマと改行区切りの2列データにしたかったのですが、どうしても2行になってしまう。pythonの勉強不足で時間切れです。
それでは、エクセルにインポートした2行のデータを行列入れ替え変換やることにしよう。

図脳rapidpro20でCSVをインポートする
図脳rapidにはCSV座標データ読込機能があり(たいていの二次元CADにはある)ので、読み込んで歯車の形状を作成。
回転やコピーは、pythonで計算するより視覚的にはるかに簡単なので、CADの独壇場ですね。
そんなわけで歯数分コピーして仮のデータ完成。
歯底円の扱いが不明。市販ギヤは円弧か角丸になっている。
歯底円で歯底を描くと、角ができてしまいます。これではエンドミルで加工できませんし、角で強度が落ちるのでRをつけなくてはいけません。
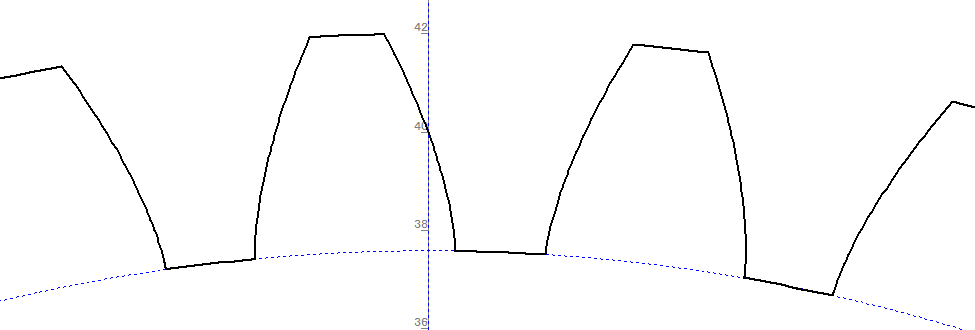
また、カッターで切り込むことを想定すると間隙は1.83mmです。φ2mmのカッターが入りませんし明らかに切り込みすぎです。
歯の谷のセンターが歯底円に接していれば、両側は立ち上がっていてもよいようです。相手歯先が当たらないギリギリまで立ち上がる円弧を見つければよい、という結論に。
そこで相手歯車を回転させながら歯の当たりを確認し、一番深い当たり半径よりも0.2mm余裕を持った円(下図の理想円)を見つけだし、図面上で回転させて歯当たりを確認しました(といっても、大歯車を1°ずつ回転させた図面を9枚作り、一番近いものをさらにコンマ数度で追い込んでいく力業です)。
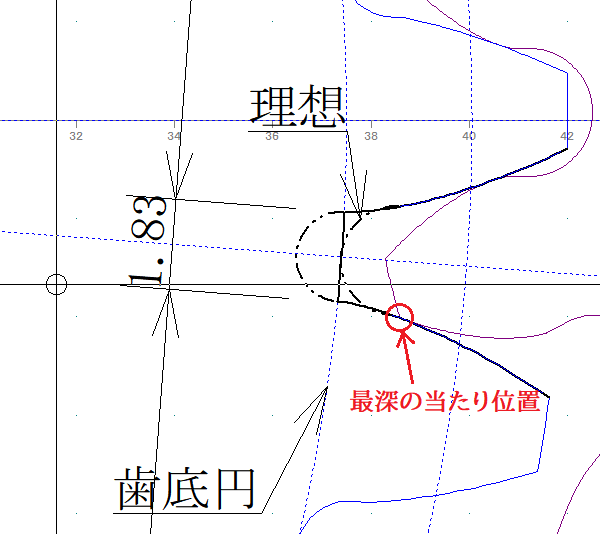
歯底円を切り込むと2mmカッター使えない 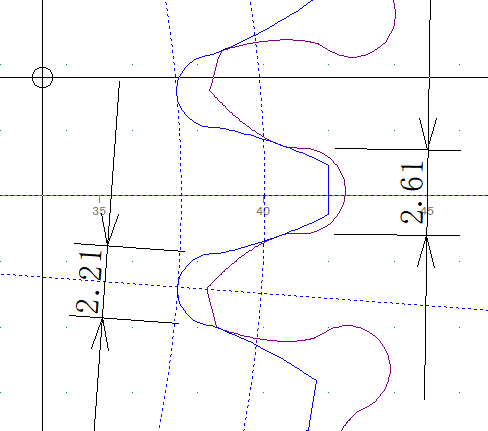
調整した結果、2mmカッター使えるようになった
この調整した円弧はギリギリにすると相手歯数によってかわることも考えられるので毎回確認したほうが良いと思われます。
バックラッシどうする?
図面は理論値なので、完全に歯筋が一致しますので、バックラッシがありません。相手方が市販ピニオンの場合はバックラッシはピニオン仕様の1/2と考えてよいのか?
切削データを作るときに考えましょうか。
というわけで、大歯車と小歯車のdxfファイルです。
1°づつずらした歯先のアニメーションです。
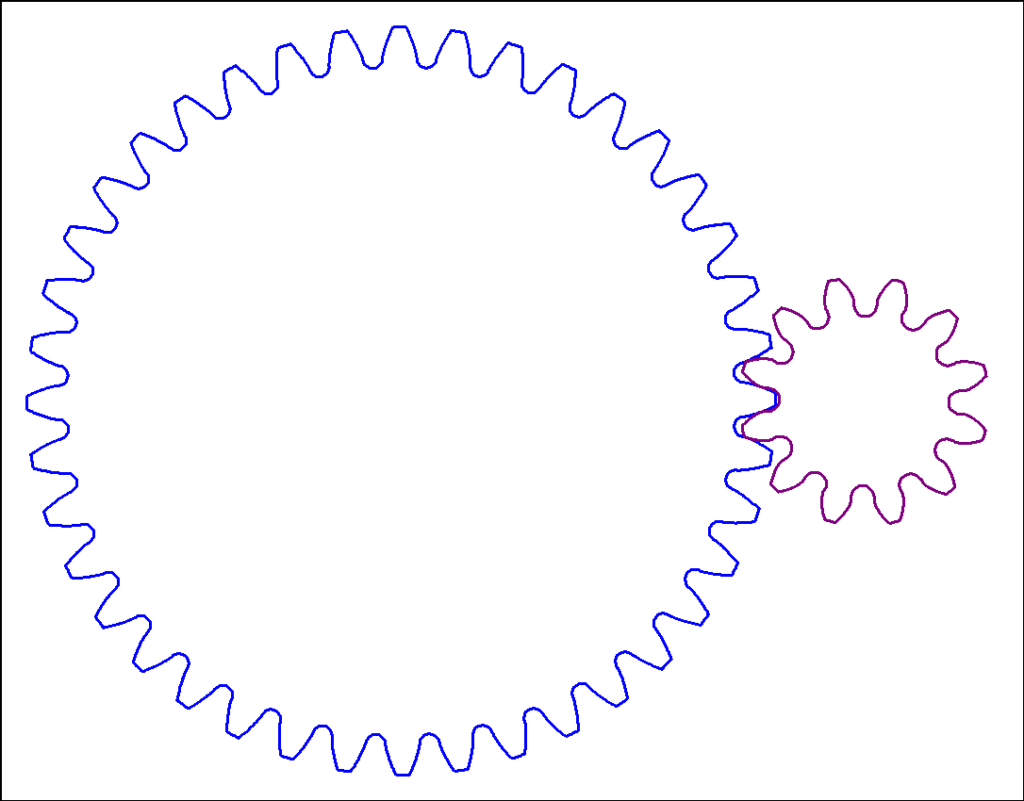
歯先部分拡大です。

続く・・・
